728x90
반응형
📌 재귀 알고리즘의 기본
📚 재귀(recursive) 알아보기
- 어떤 이벤트에서 자기 자신을 포함하고 다시 자기 자신을 사용하여 정의되는 경우
- 재귀를 효과적으로 사용하면 프로그램을 간결하고 효율성 있게 작성
📚 팩토리얼
- = 순차 곱셈
- 팩토리얼 : 양의 정수를 순서대로 곱한다는 의미
팩토리얼 n! 의 정의 (n은 양의 정수)
- 0! = 1
- n > 0이면 n! = n * (n - 1)!
# 양의 정수 n의 팩토리얼 구하기
def factorial(n: int) -> int:
"""양의 정수 n의 팩토리얼 값을 재귀적으로 구함"""
if n > 0:
return n * factorial(n - 1)
else:
return 1
if __name__ == '__main__':
n = int(input('출력할 팩토리얼 값을 입력하세요: '))
print(f'{n}의 팩토리얼은 {factorial(n)}입니다')- 매개변수 n에 전달받은 값이 0보다 크면 n * factorial(n - 1) 값을 반환
- 그렇지 않으면 1을 반환
- 파이썬에서는 표준 라이브러리인 math 모듈에서 factorial( ) 함수를 제공
📃 재귀 호출
- factorail( ) 함수는 n - 1의 팩토리얼 값을 구하기 위해 다시 자신과 똑같은 factorial( ) 함수를 호출
- 이러한 함수의 호출을 재귀 호출(recursive call)
📃 직접 재귀와 간접 재귀
- 직접(direct) 재귀 : 자신과 똑같은 함수를 호출
- 간접(indirect) 재귀 : a( ) 함수가 b( )함수를 호출하고, 다시 b( ) 함수가 a( ) 함수를 호출
📚 유클리드 호제법 알아보기
- 두 정숫값의 최대 공약수를 재귀적으로 구하는 방법
- 최대공약수 = GCD = Greatest Common Divisor
예를 들어 두 정수 x, y의 최대 공약수(gcd(x, y))를 구하고 싶은 경우
- x = az, y = bz 이며, a, b와 최대 정수 z가 존재할 때 z = gcd(x, y)
- y = 0 : x
- y ≠ 0 : gcd(y, x%y)
# 유클리드 호제법으로 최대 공약수 구하기
def gcd(x: int, y: int) -> int:
"""정숫값 x와 y의 최대 공약수를 반환"""
if y == 0:
return x
else:
return gcd(y, x % y)
if __name__ == '__main__':
print('두 정숫값의 최대 공약수를 구합니다')
x = int(input('첫 번재 정숫값을 입력하세요: '))
y = int(input('두 번재 정숫값을 입력하세요: '))
print(f'두 정숫값의 최대 공야굿는 {gcd(x, y)}입니다')
📌 재귀 알고리즘 분석
📚 재귀 알고리즘의 2가지 방법
recur( ) 라는 재귀 함수를 작성하여 재귀 알고리즘에 대해 알아봅시다
# 순수한 재귀 함수 구현하기
def recur(n: int) -> int:
"""순수한 재귀 함수 recur의 구현"""
if n > 0:
recur(n - 1)
print(n)
recur(n - 2)
x = int(input('정숫값을 입력하세요: '))
recur(x)- 재귀 호출을 여러 번 실행하는 함수
- 재귀 호출하는 함수를 하향식(top-down)과 상향식(bottom-up) 방법으로 분석
📃 하향식 분석
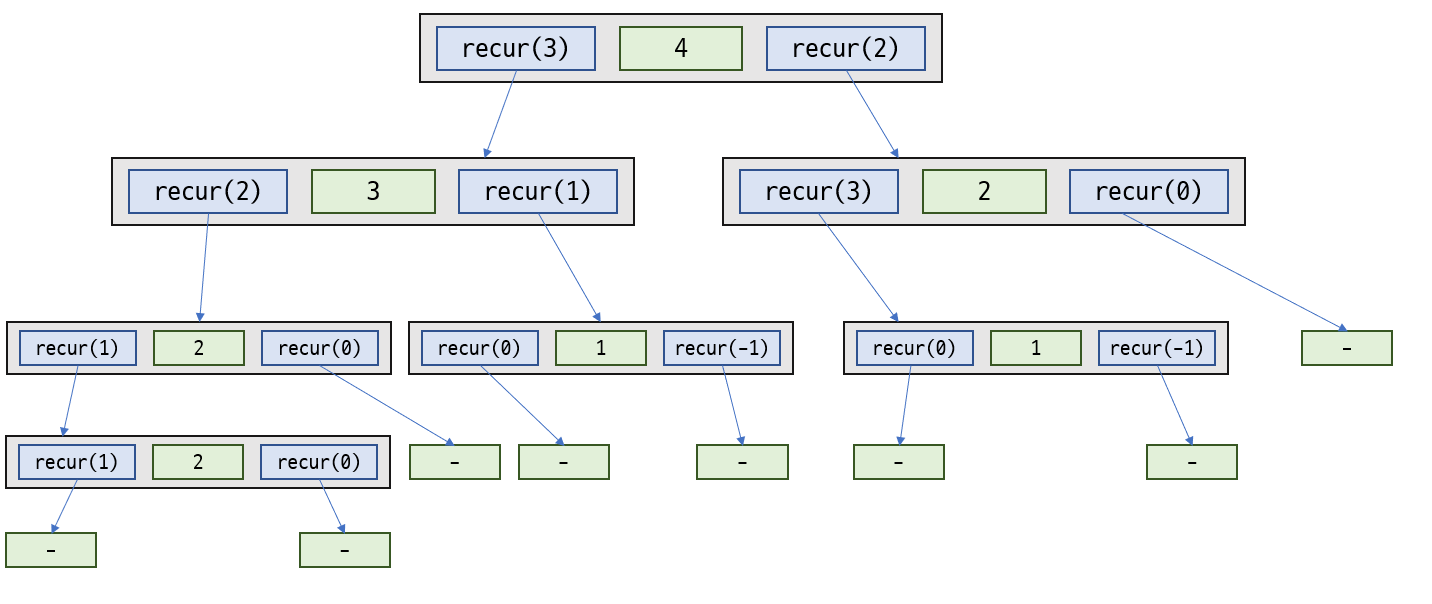
- 왼쪽 아래 화살표를 따라 갑니다
- 되돌아오면 초록색 상자 안의 값을 출력합니다
- 오른쪽 아래 화살표를 따라 갑니다
- 위의 분석 방법이 하향식 분석(top-down analysis)
- 가장 위쪽에 위치한 상자의 함수 호출부터 시작하여 계단식으로 조사
- 꼭대기부터 분석하면 같은 함수를 여러번 호출하므로 효율적이지 않을 수 있음
📃 상향식 분석
- 하향식 분석과 반대로 아래쪽부터 쌓아 올리며 분석하는 방법
- bottom-up analysis

📃 꼬리 재귀 제거하기
- recur() 함수의 뒤쪽 recur(n-2)를 변경해 꼬리 재귀를 제거
- n의 값을 n - 2로 업데이트하고 함수의 시작지점으로 돌아가도록 함
# 비재귀적으로 재귀 함수 구현하기(꼬리 재귀를 제거)
def recur(n: int) -> int:
"""꼬리 재귀를 제거한 recur() 함수"""
while n > 0:
recur(n - 1)
print(n)
n = n- 2
x = int(input('정숫값을 입력하세요: '))
recur(x)
📃 재귀를 제거하기
- 앞선 논리를 활용하여 recur(n - 1)을 제거할 수는 없습니다
- n 값을 n - 1로 업데이트하고 함수 시작 지점으로 돌아갑니다 (X)
- 현재의 n 값을 임시로 저장해서 출력해야하는 문제가 발생
- ⇒ 이는 스택(stack)으로 해결 가능
# 스택으로 재귀 함수 구현하기(제귀를 제거)
from stack import Stack
def recur(n: int) -> int:
"""재귀를 제거한 recur() 함수"""
s = Stack(n)
while True:
if n > 0:
s.push(n) # n값을 푸시
n = n - 1
continue
if not s.is_empty(): #스택이 비어있지 않으면
n = s.pop() # 저장한 값을 n에 팝
print(n)
n = n - 2
continue
break
x = int(input('정숫값을 입력하세요: '))
recur(x)
📌 하노이의 탑
# hanoi.pyy
# 하노이탑 구현하기
def move(no: int, x: int, y: int) -> None:
"""원반 no개를 x기둥에서 y기둥으로 옮김"""
if no > 1:
move(no - 1, x, 6 - x - y)
print(f'원반 [{no}]을(를) {x}기둥에서 {y}기둥으로 옮깁니다.')
if no > 1:
move(no - 1, 6 - x - y, y)
print('하노이의 탑을 구현합니다')
n = int(input('원반의 개수를 입력하세요: '))
move(n, 1, 3) # 1기둥에 쌓인 원반 n개를 3기둥으로 옮김- 기둥 번호를 정숫값 1, 2, 3으로 나타냄
- 기둥 번호의 합이 6이므로 시작 기둥과 목표 기둥을 6-x-y로 구함
📌 8퀸 문제
📚 8퀸 문제 알아보기
- 재귀 알고리즘을 설명할 때 자주 나오는 예제
8개의 퀸이 서로 공격하여 잡을 수 없도록 8 x 8 체스판에 배치할 것
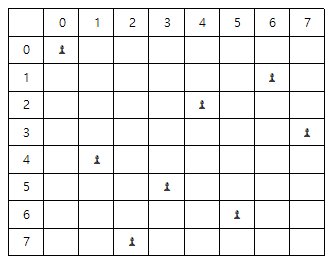
📚 퀸 배치하기
체스판 전체 조합의 수는
64 * 63 * 62 * 61 * 60 * 59 * 58 * 57=178,462,987,637,760
1. 각 열에 퀸을 1개만 배치합니다.
=> 8 * 8 * 8 * 8 * 8 * 8 * 8 * 8 = 16,777,216
2. 각 행에 퀸을 1개만 배치합니다.
=> 262,144 가지의 조합 생략 가능
📚 분기 작업으로 문제 해결하기
- 나누는 작업을 프로그램 용어로 “분기”라하고 함
- 분기(branching) 작업
- 차례대로 가지가 뻗어 나가듯이 배치 조합을 열거하는 방법
- 분할 정복법(divide and conqure, 분할해결법)
- 큰 문제를 작은 문제로 분할하고 작은 무넺 풀이법을 결합하여 전체 결합법을 얻는 방법
# 각 열에 퀸을 1개 배치하는 조합을 재귀적으로 나열하기
pos = [0] * 8
def put() -> None:
"""각 열에 배치한 퀸의 위치를 출력"""
for i in range(8):
print(f'{pos[i]:2}', end='')
print()
def set(i: int) -> None:
"""i열에 퀸을 배치"""
for j in range(8):
pos[i] = j
if i == 7:
put()
else:
set(i+1)
set(0)- 배열 pos는 퀸의 배치를 표현
- i열에 배치한 퀸의 위차가 j행에 있다면 pos[i]의 값은 j
- set( )은 pos[i] 에 차례대로 값을 대입하는 재귀함수
📚 한정 작업과 분기 한정법
- 한정(bounding) 작업
- 필요하지 않은 분기를 없애서 불필요한 조합은 열거하지 않는 방법
- 분기 한정법(branching and bounding method)
- 분기 작업과 한정 작업을 조합하여 문제 풀이를 하는 방법
# 각 열에 퀸을 1개 배치하는 조합을 재귀적으로 나열하기
pos = [0] * 8
flag = [False] * 8
def put() -> None:
"""각 열에 배치한 퀸의 위치를 출력"""
for i in range(8):
print(f'{pos[i]:2}', end='')
print()
def set(i: int) -> None:
"""i열에 퀸을 배치"""
for j in range(8):
if not flag[j]:
pos[i] = j
if i == 7:
put()
else:
flag[j] = True
set(i + 1)
flag[j] = False
set(0)- flag라는 배열을 이용해 같은 행에 중복하여 퀸을 배치하지 않도록 함
- 배치된 행에는 True가 되어 변경
- 재귀 호출한 set(i + 1) 함수가 끝나면 퀸을 j행에서 제거해서 flag[j]에 아직 배치되지 않음을 나타내는 False를 대입
📚 8퀸 문제 해결 프로그램 만들기
- 대각선 방향으로도 움직일 수 있으므로 체크 필요
- flag_b는 ↗↙ 방향을 체크. flab_c는 ↖↘을 체크
# 각 열에 퀸을 1개 배치하는 조합을 재귀적으로 나열하기
pos = [0] * 8 # 각 열에 배치한 퀸의 위치
flag_a = [False] * 8 # 각 행에 퀸을 배치했는지 체크
flag_b = [False] * 15 # 대각선 방향(↗↙)으로 퀸을 배치했는지 체크
flag_c = [False] * 15 # 대각선 방향(↖↘)으로 퀸을 배치했는지 체크
def put() -> None:
"""각 열에 배치한 퀸의 위치를 출력"""
for i in range(8):
print(f'{pos[i]:2}', end='')
print()
def set(i: int) -> None:
"""i열의 알맞은 위치에 퀸을 배치"""
for j in range(8):
if ( not flag_a[j] # j행에 퀸이 배치 되지 않았다면
and not flag_b[i + j] # 대각선 방향(↗↙)으로 퀸을 배치 되지 않았다면
and not flag_c[i - j + 7]): # 대각선 방향(↖↘)으로 퀸을 배치 되지 않았다면
pos[i] = j # 퀸을 j행에 배치
if i == 7: # 모든 열에 퀸 배치 완료
put()
else:
flag_a[j] = flag_b[i + j] = flag_c[i - j + 7] = True
set(i + 1) # 다음 열에 퀸을 배치
flag_a[j] = flag_b[i + j] = flag_c[i - j + 7] = False
set(0)- 퀸이 배치된 상태를 더 쉽게 알아보기 위해서는 다음의 함수를 사용하면 됩니다.
def put() -> None:
"""퀸의 배치를 ■와 □으로 출력"""
for j in range(8):
for i in range(8):
print('■' if pos[i] == j else '□', end='')
print()728x90
반응형
'코딩 테스트 > 파이썬 알고리즘' 카테고리의 다른 글
| [코테 알고리즘] 파이썬 기본 / 관련 문제 (0) | 2024.03.07 |
|---|---|
| 복잡도 정리 (0) | 2023.09.30 |
| [구버전] [Python] 03. 스택과 큐 (0) | 2023.01.14 |
| [구버전] [Python] 02. 검색 알고리즘 (0) | 2023.01.09 |
| [구버전] [Python] 01. 자료 구조와 배열 (0) | 2023.01.04 |

